Kapitel 7 Deskriptive Statistik
In diesem Kapitel geht es um die deskriptive (beschreibende) Statistik. Mit dieser Art von Statistik kann man Aussagen über die Verteilung von Merkmalen in Stichproben treffen. Zum Testen von Hypothesen ist sie nicht geeignet, aber es ist in jedem Fall sinnvoll, sich zunächst einen Überblick über die Verteilung von Variablen im Datensatz zu machen. Dazu ist deskriptive Statistik sehr hilfreich. In diesem Abschnitt werden deshalb die folgenden Themen behandelt:
- Häufigkeitsverteilungen (inkl. Säulendiagram)
- Maße der zentralen Tendenz und Streuung
- Schiefe und Kurtosis
- Funktionen zur Anzeige mehrere Kennwerte und mehrere Variablen
7.1 Datensatz für dieses Kapitel
Als Datensatz dient in diesem Kapitel wieder der “starwars”-Datensatz, der im Paket dplyr enthalten ist. Er enthält verschiedene Merkmale von Starwars-Figuren:
starwars## # A tibble: 87 x 14
## name height mass hair_color skin_color eye_color birth_year sex gender
## <chr> <int> <dbl> <chr> <chr> <chr> <dbl> <chr> <chr>
## 1 Luke S… 172 77 blond fair blue 19 male mascu…
## 2 C-3PO 167 75 <NA> gold yellow 112 none mascu…
## 3 R2-D2 96 32 <NA> white, bl… red 33 none mascu…
## 4 Darth … 202 136 none white yellow 41.9 male mascu…
## 5 Leia O… 150 49 brown light brown 19 fema… femin…
## 6 Owen L… 178 120 brown, grey light blue 52 male mascu…
## 7 Beru W… 165 75 brown light blue 47 fema… femin…
## 8 R5-D4 97 32 <NA> white, red red NA none mascu…
## 9 Biggs … 183 84 black light brown 24 male mascu…
## 10 Obi-Wa… 182 77 auburn, wh… fair blue-gray 57 male mascu…
## # … with 77 more rows, and 5 more variables: homeworld <chr>, species <chr>,
## # films <list>, vehicles <list>, starships <list>7.2 Häufigkeitsverteilung
7.2.1 Tabellen
Es gibt in den unterschiedlichen R-Paketen sehr viele Möglichkeiten, sich eine Häufigkeitsverteilung ausgeben zu lassen. Die schnellste und einfachste Möglichkeit ist die Funktion table(), die in base R verfügbar ist. Man kann sie also nutzen, ohne zusätzliche Pakete zu laden. Als Argument benötigt die Funktion lediglich einen Verweis auf den Vektor, der tabuliert werden soll (also auf den Datensatz und die entsprechende Variable).
# Häufigkeitstabelle, absolute Zahlen
table(starwars$sex)##
## female hermaphroditic male none
## 16 1 60 6Das Ergebnis ist wirklich sehr basic. Es werden standardmäßig nur die absoluten Häufigkeiten ausgegeben und fehlende Werte werden weggelassen. Letztere kann man über das Argument useNA = "ifany" mit ausgeben lassen:
# Häufigkeitstabelle, absolute Zahlen
table(starwars$sex, useNA = "ifany")##
## female hermaphroditic male none <NA>
## 16 1 60 6 4Neben dem sehr schlichten table()-Befehl gibt in vielen R-Paketen weitere Tabulierungs-Funktionen, mit denen man sich umfangreichere und übersichtlichere Häufigkeitstabellen ausgeben lassen kann. Diese Funktionen unterscheiden sich jeweils leicht in den Informationen, die sie anzeigen. An dieser Stelle möchte ich beispielhaft die Funktion tabyl()aus dem Paket janitor vorstellen. Ich habe sie hier ausgewählt, weil ich das janitor-Paket zum Datenmanagement ohnehin häufig nutze und weil hier die Prozentwerte einmal mit und einmal ohne fehlende Werte ausgegeben werden.
library(janitor)
tabyl(starwars$sex)## starwars$sex n percent valid_percent
## female 16 0,18390805 0,19277108
## hermaphroditic 1 0,01149425 0,01204819
## male 60 0,68965517 0,72289157
## none 6 0,06896552 0,07228916
## <NA> 4 0,04597701 NASchon sehr viel übersichtlicher und informativer! Allerdings fehlen noch Spalten für die kumulierten Prozentwerte. Diese Spalten können wir mit mutate() aus dem tidyverse leicht selbst berechnen (siehe Kapitel zur Datenaufbereitung). Zusätzlich brauchen wir die Funktion cumsum(), welche kumulierte Summen bildet.
library(tidyverse)
tabyl(starwars$sex) %>%
# fügt Spalte für kumulierte Prozent und eine für kumulierte, gültige Prozent ein
mutate(cum_percent = cumsum(percent),
cum_valid_percent = cumsum(valid_percent)) ## starwars$sex n percent valid_percent cum_percent cum_valid_percent
## female 16 0,18390805 0,19277108 0,1839080 0,1927711
## hermaphroditic 1 0,01149425 0,01204819 0,1954023 0,2048193
## male 60 0,68965517 0,72289157 0,8850575 0,9277108
## none 6 0,06896552 0,07228916 0,9540230 1,0000000
## <NA> 4 0,04597701 NA 1,0000000 NA7.2.2 Häufigkeitsdiagramm
Statistische Grafiken/Plots sind in R flexibel gestaltbar und können in Druckqualität ausgegeben werden. Im späteren Kapitel “Darstellung” gehe ich nochmal genau darauf ein, wie man Grafiken hübsch machen kann. Darum geht es an dieser Stelle aber noch nicht. Denn im Rahmen der Exploration von Datensätzen ist es zunächst erstmal wichtig, dass Sie die Grafik dazu benutzen, sich einen Überblick zu verschaffen! Eine besonders ausgefeilte - und möglicherweise aufwendige Formatierung - ist an dieser Stelle nicht nötig.
Zur Erstellung von Plots ist das Paket ggplot aus dem tidyverse mittlerweile ein ziemlicher Standard. Leider ist die Syntax etwas ungelenk und es ist etwas herausfordernd, damit tatsächlich schöne Grafiken zu bauen. Wenn man Grafiken später in einen Forschungsbericht einbauen möchte, lohnt es sich auf jeden Fall in ggplot einzusteigen. Ich werde Ihnen den Umgang mit dem Paket in einem späteren Kapitel auch noch vorstellen. Für die explorative Analyse und den schnellen Überblick eignet sich das Paket sjPlot sehr gut, weil es ohne viele Befehle akzeptable Grafiken produziert. Es basiert im Hintergrund auf ggplot2, übernimmt aber das Formatieren vollautomatisch. Die Syntax für ein Säulendiagramm, wie wir es für unsere Häufigkeitsauszählung benötigen ist deshalb sehr simpel:
library(sjPlot)
plot_frq(starwars$sex, sort.frq = "desc")## Warning: `guides(<scale> = FALSE)` is deprecated. Please use `guides(<scale> =
## "none")` instead.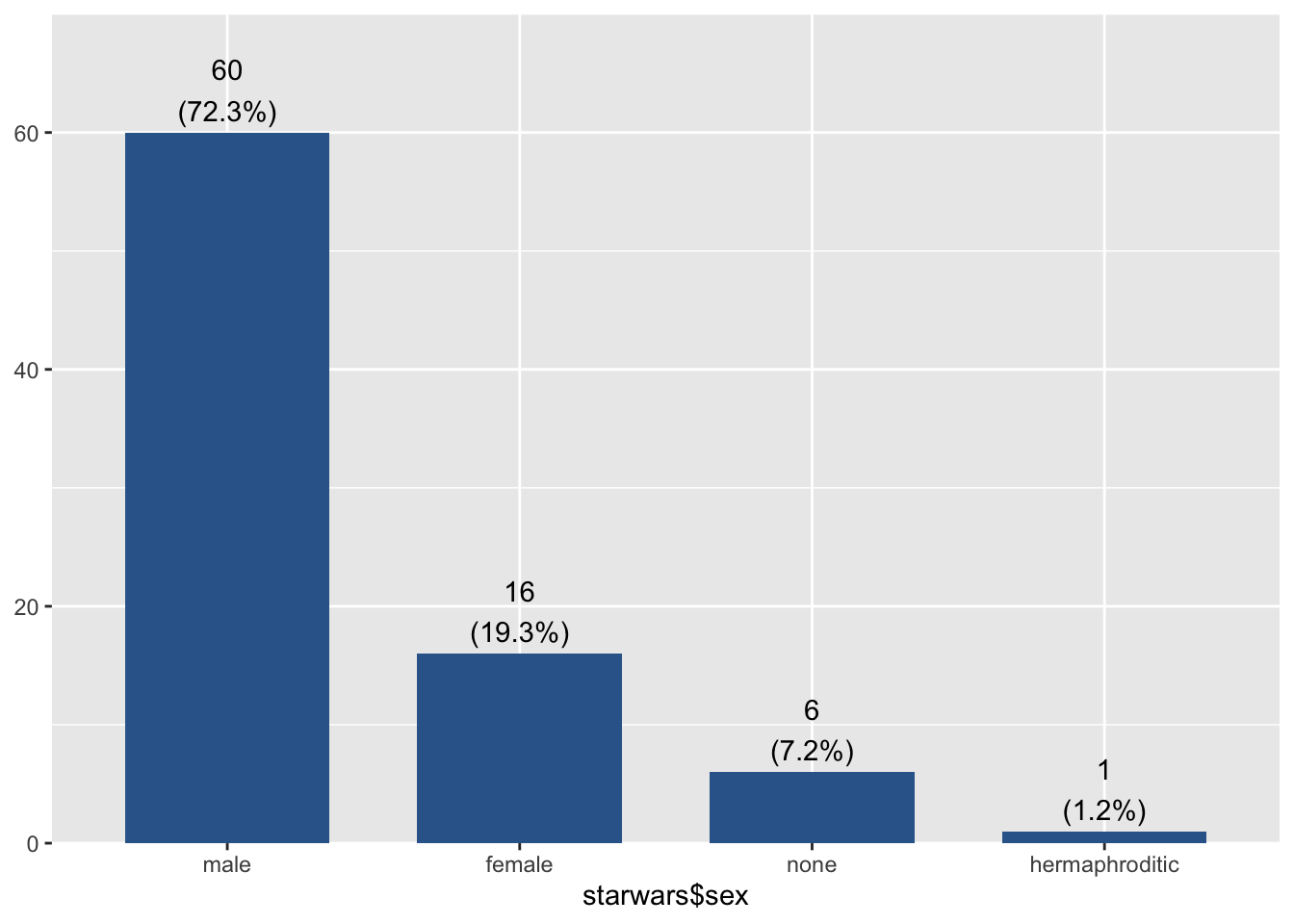
Das Argument sort.frq = "desc" sorgt für eine absteigende Sortierung der Balken. Es ist natürlich nur bei nominalen Daten sinnvoll.
Über die Funktion plot_frq() sind noch weitere Darstellungsformen möglich, wie beispielsweise ein Liniendiagramm oder ein Diagramm mit Punkten. Man muss dazu lediglich das zusätzliche Argument type mit an die Funktion übergeben (z.B. type = "line" oder type = "dot"). Auch Histogramme sind möglich (type = "histogram):
library(sjPlot)
plot_frq(starwars$mass, type = "histogram")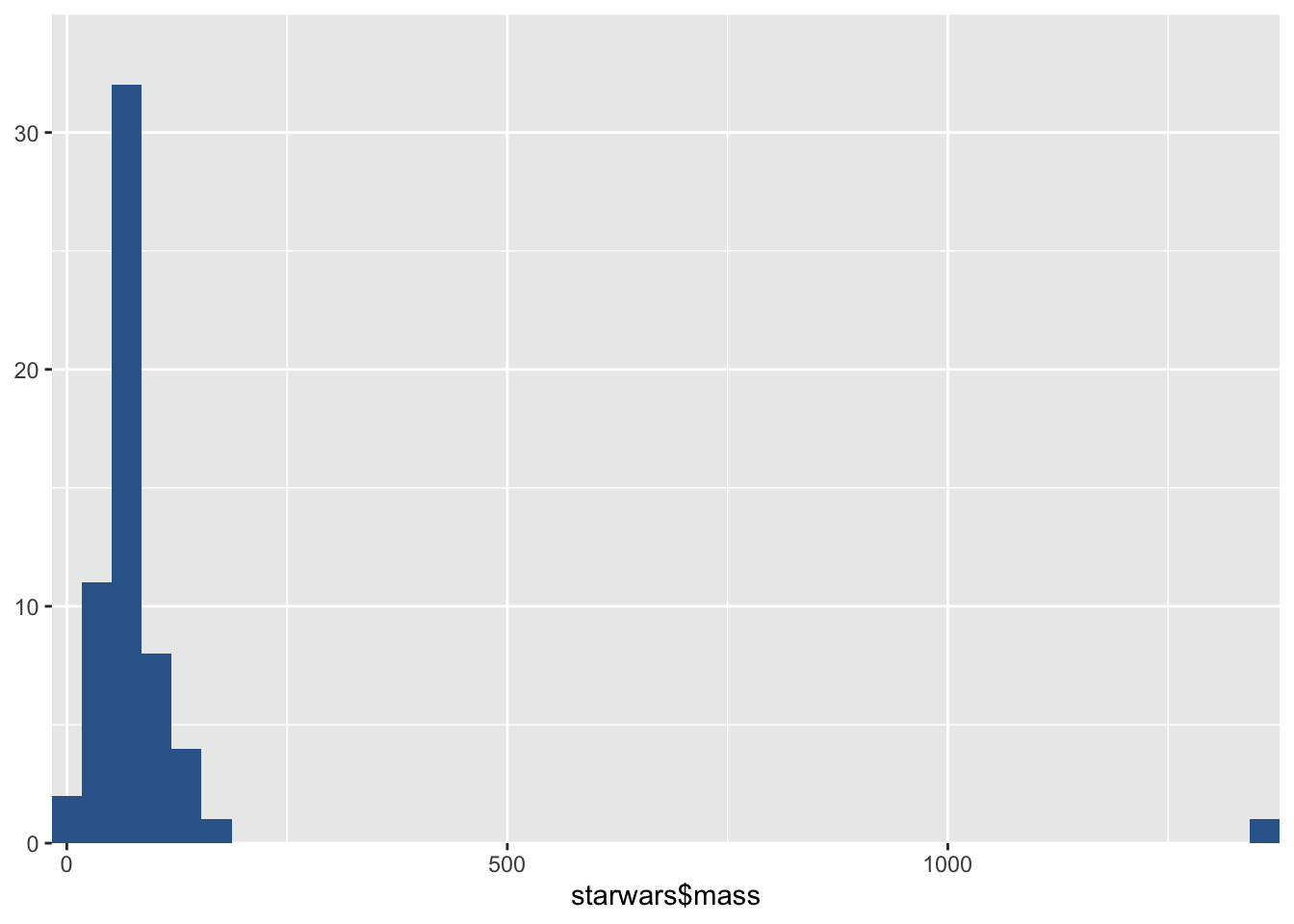
Das Histogramm offenbart in der Variable mass einen extremen Ausreißer, der sehr viel schwerer ist als alle anderen Starwars-Figuren.
7.3 Maße der zentralen Tendenz & Streuung
Neben Häufigkeitsauszählungen dienen Maße der zentralen Tendenz und Streuung dazu, die Eigenschaften von Variablen sehr kompakt zu beschreiben. Ich ordne die Maßzahlen hier nach Datenniveau, beginnend bei niedrigsten bis zum höchsten. Selbstverständlich können Sie die Maße für ein niedrigeres Datenniveau auch für höhere Datenniveaus anwenden. Umgekehrt ist das jedoch nicht sinnvoll! Allerdings kennt R das Datenniveau der Variablen nicht. Es wird also ohne Probleme und Fehlermeldung auch ein arithmetisches Mittel für eine nominale Variable ausgeben, falls diese mit Zahlen codiert wurde (bei reinen character-Variablen geht das selbstverständlich nicht). Das Denken kann uns R an dieser Stelle also leider nicht abnehmen. Wir müssen immer selbst vorab beurteilen, ob eine Berechnung sinnvoll ist oder nicht.
7.3.1 Nominale Daten
Als Beispiel für eine nominale Variable verwende ich die Frage, welches Geschlecht die Starwars-Figuren haben. Die Variable hat die folgenden Ausprägungen:
sjlabelled::get_labels(starwars$sex)## [1] "male" "none" "female" "hermaphroditic"
## [5] NADer Modus ist der Wert in einer Verteilung, der am häufigsten vorkommt. Da die Reihenfolge der Ausprägungen dabei keine Rolle spielt, ist er sogar für nominale Daten anwendbar. Man kann ihn aber auch für ordinale und metrische Daten ermitteln.
Für den Modus gibt es in base-R keine Standard-Funktion, vielleicht ist er einfach zu simpel. Man kann den Modus einfach über eine Häufigkeitsauszählung ermitteln oder über ein Säulendiagram (siehe voriger Abschnitt).
Alternativ gibt es noch eine Mode()-Funktion im DescTools-Paket. Achtung! Das Paket ist etwas altmodisch bei der Benennung seiner Funktionen: Mode() muss hier zwingend groß geschrieben werden!! Außerdem liefert die Funktion kein Ergebnis zurück, wenn es zwei gleich hohe höchste Ausprägungen gibt.
library(DescTools)
Mode(starwars$sex, na.rm = TRUE)## [1] "male"
## attr(,"freq")
## [1] 60Die Funktion liefert gleich zwei Ergebnisse zurück: Zum einen den Wert, der die meisten Ausprägungen auf sich vereint, in diesem Fall die Ausprägung “male.” Zum anderen die absolute Häufigkeit, die diese Ausprägung hat (n = 60).
7.3.2 Ordinale Daten
Der Median teilt die (sortierten) Fälle einer Variablen in zwei gleich große Hälften. Er kann für ordinale und metrische Daten berechnet werden.
Die Funktion für den Median gibt es sogar in base-R. Sie heißt schlicht median(). Die Funktion benötigt zwei Argumente. Zum einen selbstverständlich den Verweis auf die Variable und zum anderen einen Hinweis, wie mit fehlenden Werten umgegangen werden soll. Da R nicht wissen kann, wie fehlende Werte einzuberechnen wären, müssen sie vorab aus der Analyse entfernt werden, mit na.rm = TRUE (NA remove).
Im Datensatz gibt es keine ordinale Variable, deshalb nehme ich im folgenden die Größe in cm (metrisch) als Beispiel:
median(starwars$height, na.rm = TRUE)## [1] 180Die Spannweite (range) gibt an, zwischen welchen Ausprägungen sich eine Variable bewegt, also den höchsten und den niedrigsten Wert.
range(starwars$height, na.rm = TRUE)## [1] 66 264Über die Funktionen min() und max() kann man sich übrigens auch einzeln das Minimum bzw. Maximum ausgeben lassen.
Wie oben erwähnt, teilt der Median die Verteilung der Werte in zwei gleiche Hälften. Wenn man jedoch nicht zwei Hälften haben möchte, sondern sich eher für Drittel, Viertel oder Fünftel interessiert, sind Quantile das Mittel der Wahl. Üblich sind eigentlich nur Quartile, also die Einteilung in Viertel. Deshalb gibt die base-R-Funktion quantile() standardmäßig die Grenzen der Quartile zurück.
quantile(starwars$height, na.rm = TRUE)## 0% 25% 50% 75% 100%
## 66 167 180 191 264Es handelt sich um 5 Grenzen, weil der niedrigste und der höchste Wert mit ausgegeben werden. Die Quartile befinden sich quasi “zwischen” diesen 5 Grenzpunkten.
Der **Interquartilsabstand* gibt den Abstand zwischen dem Ende des ersten und dem Beginn des letzten Quartils an, also in unserem Beispiel den Abstand zwischen den Ausprägungen 167 und 191 cm (= 24 cm).
IQR(starwars$height, na.rm = TRUE)## [1] 247.3.3 Metrische Daten
Für metrische Variablen haben Sie die Auswahl zwischen allen hier vorgestellten Maßen der zentralen Tendenz (wobei der Modus in der Regel bei vielen Ausprägungen kaum Sinn macht). Üblich ist vor allem das “arithmetische Mittel”, umgangssprachlich oft auch als Durchschnitt oder Mittelwert bezeichnet. Die Funktion mean() habe ich in den Einführungskapiteln bereits als Beispiel genutzt.
Als Beispiel benutze ich hier die Variable für das Gewicht.
mean(starwars$mass, na.rm = TRUE)## [1] 97,31186Das Durschnittsgewicht im Sample beträgt also 97.31 Einheiten (kg?).
Man kann sich auch ein getrimmtes Mittel ausgeben lassen, bei dem die oberen und niedrigen X Prozent der Daten entfernt werden. So kann das arithmetische Mittel robust gemacht werden gegen Extremwerte. Aus dem Abschnitt über die Häufigkeiten (Histogram) wissen wir, dass es in der Variable einen extremen Ausreißer gibt. Ein Starwars-Charakter ist viel schwerer als alle anderen. Er verzerrt das arithmetische Mittel nach oben. Ein getrimmtes Mittel liefert deshalb vielleicht ein realistischeres Bild:
mean(starwars$mass, trim = 0.1, na.rm = TRUE)## [1] 75,43673Es macht Sinn, sich bei einer Variable nie allein das arithmetische Mittel anzusehen. Sie wüssten dann z.B. nicht ob ein Wert (z.B. 80 kg) nur erreicht wird, weil alle Befragten genau so schwer sind, weil es sehr viele Personen mit 75 und 85 kg im Sample gibt oder eine ganz andere Verteilung vorherrscht. Wie der Name schon sagt, geben Streuungsmaße Auskunft darüber, wie die Werte einer Variablen um den Mittelwert streuen oder variieren. Das wichtigste Streuungsmaß, welches auch immer gemeinsam mit dem arithmetischen Mittel angesehen und berichtet werden sollte, ist die Streuung (standard deviation).
sd(starwars$mass, na.rm = TRUE)## [1] 169,4572Die Streuung ist bekanntlich die Wurzel der Varianz und als Streuungsmaß auch um einiges üblicher. Dennoch soll hier natürlich auch die Funktion für die Varianz nicht fehlen:
var(starwars$mass, na.rm = TRUE)## [1] 28715,737.4 Schiefe und Kurtosis
Weitere Kennwerte für die Form von Verteilungen sind die Schiefe (skew) und Kurtosis (kurtosis). Die Schiefe ist quasi das Gegenteil von Symmetrie. Kurtosis drückt aus, wie spitz (nach oben gewölbt) oder flach eine Verteilung ist.
Im psych-Paket gibt es Funktionen für beides:
library(psych)
skew(starwars$height, na.rm = TRUE)## [1] -1,025488Zur Erinnerung:
Ist die Schiefe > 0 so ist die Verteilung rechtsschief (Modus < Median < arithmetisches Mittel).
Ist die Schiefe = 0, so ist die Verteilung symmetrisch (Modus = Median = arithmetisches Mittel).
Ist die Schiefe < 0 so ist die Verteilung linksschief (Modus > Median > arithmetisches Mittel).
Die Verteilung des Alters im obigen Beispiel ist also nahezu symmetrisch, ein wenig linksschief.
Hier noch der Code zur Berechnung der Kurtosis:
kurtosi(starwars$height, na.rm = TRUE)## [1] 1,7764147.5 Übersichts-Funktionen
Bisher haben wir uns die Statistiken jeweils für eine einzelne Variable ausgeben lassen. Aber natürlich macht es Sinn, sich mehrere Kennwerte gleichzeitig ausgeben zu lassen. Die Funktion summary() aus dem base-Paket liefert zum Beispiel einen guten ersten Einblick:
summary(starwars$height)## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 66,0 167,0 180,0 174,4 191,0 264,0 6Allerdings fehlen an dieser Stelle z.B. die Streuungsmaße. Es geht also noch mehr. Das vorhin genutzte psych-Paket hat z.B. eine describe()-Funktion, mit der man sich gleichzeitig verschiedene deskriptive Statistiken ausgeben kann - und zwar nicht nur für eine Variable, sondern gleich für mehrere oder sogar für einen ganzen Datensatz.
In dem nun folgenden Code habe ich den Datensatz um ein paar Variablen gekürzt ([, 1:11]), weil die Funktion describe() mit diesen Variablen nicht funktioniert.
desc_stats <- describe(starwars[, 1:11])
head(desc_stats)## vars n mean sd median trimmed mad min max range skew
## name* 1 87 44,00 25,26 44 44,00 32,62 1 87 86 0,00
## height 2 81 174,36 34,77 180 178,17 19,27 66 264 198 -1,03
## mass 3 59 97,31 169,46 79 75,44 16,31 15 1358 1343 6,97
## hair_color* 4 82 7,94 2,70 10 8,12 2,97 1 12 11 -0,58
## skin_color* 5 87 13,62 8,26 13 13,15 8,90 1 31 30 0,47
## eye_color* 6 87 6,25 4,83 4 5,86 4,45 1 15 14 0,67
## kurtosis se
## name* -1,24 2,71
## height 1,78 3,86
## mass 48,93 22,06
## hair_color* -0,83 0,30
## skin_color* -0,93 0,89
## eye_color* -1,04 0,52Da sind jetzt sogar einige Kennzahlen dabei, die wir bisher gar nicht besprochen haben (und auch nicht besprechen werden, z.B. “mad”). Über verschiedene Argumente kann man sich noch weitere Kennzahlen in der Tabelle anzeigen lassen (z.B. skew = TRUE oder ranges = TRUE). Allerdings fällt auch auf, dass die Berechnungen nicht für alle Variablen durchgeführt werden. Ein Mittelwert der Namen ist auch keine nützliche Angabe. Mit dem zusätzlichen Argument omit = TRUE kann man diese Zeilen ausblenden.
Kleine Warnung: Die RStudio-Cloud verhält sich in Bezug auf die describe()-Funktion leicht anders. Warum das so ist, weiß ich nicht.
Wichtige Funktionen aus diesem Kapitel
| Funktion | Paket | Beschreibung | Wichtige Argumente |
|---|---|---|---|
| Häufigkeiten | |||
table() |
stats | einfache Tabelle | useNA = "ifany" |
tabyl() |
janitor | Häufigkeitstabelle mit Prozent | |
plot_frq() |
sjPlot | Säulendiagramm | |
| Maße der zentralen Tendenz & Streuung | |||
Mode() |
DescTools | Modus | |
median() |
stats | Median | na.rm = TRUE |
range() |
stats | Range | na.rm = TRUE |
quantile() |
stats | Quantilgrenzen | na.rm = TRUE |
IQR() |
stats | Inter-Quartil-Range | na.rm = TRUE |
mean() |
base | Arithmetisches Mittel | na.rm = TRUE |
sd() |
stats | Standardabweichung | na.rm = TRUE |
var() |
stats | Varianz | na.rm = TRUE |
| Schiefe und Kurtosis | |||
skew() |
psych | Schiefe | na.rm = TRUE |
kurtosi() |
psych | Kurtosis | na.rm = TRUE |
| Übersichts-Funktionen | |||
summary() |
base | Wichtige Verteilungsmerkmale | |
describe() |
psych | Tabelle deskriptiver Merkmale |